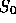 . At
time
. At
time  , the price has moved to either
, the price has moved to either  , or
, or
 . The risk free interest rate is such that $1 now will
be worth $
. The risk free interest rate is such that $1 now will
be worth $ at time
at time 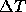 .
.
Michaelmas Term 1998: Problems for solution
1. Consider the following simple model of stock price
movement. The value of the stock at time zero is 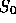 . At
time
. At
time  , the price has moved to either
, the price has moved to either  , or
, or
 . The risk free interest rate is such that $1 now will
be worth $
. The risk free interest rate is such that $1 now will
be worth $ at time
at time 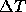 .
.
 . Show that the market price
of a European call option which matures at time
. Show that the market price
of a European call option which matures at time  with strike price K is
with strike price K is
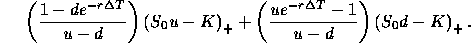
 ?
?
2. Suppose that at current exchange rates,  100 is
worth 280DM. A speculator believes that by the end of the year there
is a probability of 2/3 that the pound will have fallen to 2.60DM,
and a 1/3 chance that it will have gained to be worth 3.00DM. He
therefore buys a European put option that will give him the right
(but not the obligation) to sell
100 is
worth 280DM. A speculator believes that by the end of the year there
is a probability of 2/3 that the pound will have fallen to 2.60DM,
and a 1/3 chance that it will have gained to be worth 3.00DM. He
therefore buys a European put option that will give him the right
(but not the obligation) to sell  100 for 290DM at the end
of the year. He pays 20DM for this option. Assume that the risk free
interest rate is zero. Using a single period binary model,
either construct a
strategy whereby one party is certain to make a profit or prove that
this is the fair price.
100 for 290DM at the end
of the year. He pays 20DM for this option. Assume that the risk free
interest rate is zero. Using a single period binary model,
either construct a
strategy whereby one party is certain to make a profit or prove that
this is the fair price.
3. (Put-Call parity.)
Let us denote by  and
and 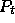 respectively the prices
of a European call and a European put option, each
with maturity T and strike K. Assume that the risk free rate of
interest is constant, r (so the cost of borrowing $1 for s units of
time is $
respectively the prices
of a European call and a European put option, each
with maturity T and strike K. Assume that the risk free rate of
interest is constant, r (so the cost of borrowing $1 for s units of
time is $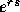 ). Show that for each
). Show that for each  ,
,

4. Suppose that the price of a certain asset has the
lognormal distribution. That is  is
normally disrtibuted with mean
is
normally disrtibuted with mean 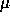 and variance
and variance  .
Calculate
.
Calculate  .
.
5. Find the risk-neutral probabilities
for the model in Question 2.
That is, find the
probabilities p, 1-p for upward/downward movement of the pound,
under which `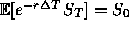 '.
Check that the fair price of the option is then
'.
Check that the fair price of the option is then  (since
r=0)
where the expectation is calculated with respect to these probabilities..
(since
r=0)
where the expectation is calculated with respect to these probabilities..
6. Consider two dates  with
with  . A forward
start option is a contract in which the holder receives at time
. A forward
start option is a contract in which the holder receives at time  ,
at no extra cost, an option with expiry date
,
at no extra cost, an option with expiry date  and strike price
equal to
and strike price
equal to  (the asset price at time
(the asset price at time  ). Assume that the
stock price evolves according to a two-period binary model, in which the
asset price at time
). Assume that the
stock price evolves according to a two-period binary model, in which the
asset price at time  is either
is either  or
or 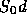 , and at time
, and at time 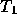 is one of
is one of  ,
,  and
and  with
with

where r denotes the risk free interest rate. Find the fair price of such an option at time zero.
7. A digital option is one in which the payoff depends in
a discontinuous way on the asset price. The simplest example is the
cash-or-nothing option, in which the payoff to the holder at
maturity T is  where X is some prespecified cash
sum.
where X is some prespecified cash
sum.
Suppose that an asset price evolves according to the
Cox Ross Rubinstein model (CRR model). That is, a multiperiod binary model
in which, at each step, the asset price moves from its current
value 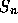 to one of
to one of  and
and 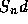 . As usual, if
. As usual, if  denotes the length of each time step,
denotes the length of each time step,
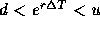 .
.
Find the time zero price of the above option. You may leave your answer as a sum.
8. Suppose that an asset price evolves according to the
CRR model described in Question 7. For simplicity suppose that
the risk free interest rate is zero and  is 1.
Suppose that under the probability
is 1.
Suppose that under the probability 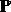 , at each time step,
stock prices go up
with probability p and down with probability 1-p.
, at each time step,
stock prices go up
with probability p and down with probability 1-p.
The conditional expectation

is a stochastic process. Check that it is a 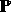 -martingale and
find the distribution of
-martingale and
find the distribution of 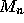 ?
?
9. Show how to derive the put-call parity relationship of Question 3 from Theorem 3.3 of lectures.
10. Let 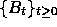 be standard Brownian motion.
Which of the following are Brownian motions?
be standard Brownian motion.
Which of the following are Brownian motions?

 , where c is a constant,
, where c is a constant,
 ,
,

11. Suppose that  is standard Brownian motion.
Prove that conditional on
is standard Brownian motion.
Prove that conditional on  , the probability density
function of
, the probability density
function of 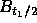 is
is
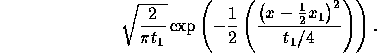
This tells us that the conditional distribution is a normally distributed random variable. What are the mean and variance?
12. Let 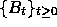 be standard Brownian motion.
Let
be standard Brownian motion.
Let  be the `hitting time of level a', that is
be the `hitting time of level a', that is

Then we shall prove in lectures that

Use this result to calculate
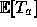 ,
,
 .
.
13. Let  denote standard Brownian motion
and define
denote standard Brownian motion
and define  by
by

Suppose that 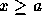 . Calculate
. Calculate
 ,
,
 .
.
14. Let  be standard Brownian motion.
Let
be standard Brownian motion.
Let  denote the hitting time of the sloping line a+bt.
That is,
denote the hitting time of the sloping line a+bt.
That is,
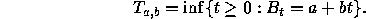
We show in lectures that

The aim of this question is to calculate the distribution of  ,
without inverting the Laplace transform.
In what follows,
,
without inverting the Laplace transform.
In what follows, 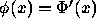 and
and
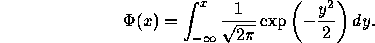
 .
.
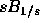 has the same distribution as
has the same distribution as 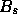 ,
show that
,
show that
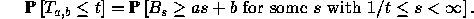
 , use the previous
part to
show that
, use the previous
part to
show that

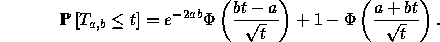
15. Let  denote the natural
filtration associated to a standard Brownian motion
denote the natural
filtration associated to a standard Brownian motion
 . Which of the following are
. Which of the following are
 -martingales?
-martingales?
 ,
,
 , where c is a constant,
, where c is a constant,
 ,
,
16. Let  denote the natural
filtration associated to a standard Brownian motion
denote the natural
filtration associated to a standard Brownian motion
 . Define the process
. Define the process  by
by

For which values of  is the process
is the process  an
an
 -martingale?
-martingale?
17.
A function, f, is said to be Lipschitz continuous on  if
there exists a constant C>0 such that for any
if
there exists a constant C>0 such that for any 

Show that a Lipschitz continuous function has bounded variation and zero quadratic variation.
18. Let  denote standard Brownian motion.
For a partition
denote standard Brownian motion.
For a partition  of
of  , write
, write  for the mesh
of the partition and
for the mesh
of the partition and  for the number of intervals. We write
for the number of intervals. We write
 to denote a generic subinterval in the partition.
Calculate
to denote a generic subinterval in the partition.
Calculate

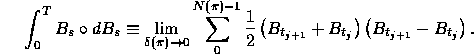
This is the Stratonovich integral of  with respect to itself.
with respect to itself.
19. Suppose that  is a function of bounded quadratic
variation on
is a function of bounded quadratic
variation on  , and
, and 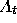 is a Lipschitz continuous function
on
is a Lipschitz continuous function
on  . Using
. Using  to denote the quadratic variation
of a function f over the interval
to denote the quadratic variation
of a function f over the interval  , show that
, show that

20. If f is a simple function, prove that the process
 given by the Itô integral
given by the Itô integral

is a martingale.
21. Verify that
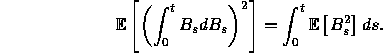
(If you need the moment generating function of 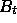 , you may assume
the result of Question 23.)
, you may assume
the result of Question 23.)
22. Use Itô's formula to write down stochastic differential
equations for the following quantities. (As usual, 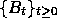 denotes standard Brownian motion.)
denotes standard Brownian motion.)
 ,
,
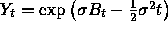 ,
,
 .
.
23. Let  denote Brownian motion and
define
denote Brownian motion and
define 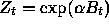 . Use Itô's formula to write
down a stochastic differential equation for
. Use Itô's formula to write
down a stochastic differential equation for  . Hence find
an ordinary (deterministic) differential equation for
. Hence find
an ordinary (deterministic) differential equation for
 , and solve to show that
, and solve to show that
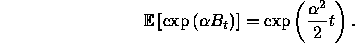
24. (The Ornstein-Uhlenbeck process).
Let  denote standard Brownian motion.
The Ornstein-Uhlenbeck process,
denote standard Brownian motion.
The Ornstein-Uhlenbeck process, 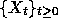 is the
unique solution to Langevin's equation,
is the
unique solution to Langevin's equation,

This equation was originally introduced as a simple idealised model for the velocity of a particle suspended in a liquid. Verify that

and use this expression to calculate the mean and variance of 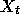 .
.
25. Suppose that under the probability measure  ,
,
 is a Brownian motion with constant drift
is a Brownian motion with constant drift  .
Find a measure
.
Find a measure  , equivalent to
, equivalent to  , under which
, under which
 is a Brownian motion with drift
is a Brownian motion with drift  .
.
26.
Suppose that an asset price  is such that
is such that
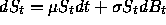 ,
where
,
where 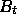 is,
as usual, standard Brownian motion. Let r denote
the risk free interest rate. The price of a riskless asset then follows
is,
as usual, standard Brownian motion. Let r denote
the risk free interest rate. The price of a riskless asset then follows
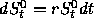 .
We write
.
We write  for the portfolio consisting of
for the portfolio consisting of 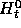 units
of the riskless asset,
units
of the riskless asset,  , and
, and 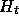 units of
units of  at time t.
For each of the following choices of
at time t.
For each of the following choices of 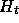 , find
, find  so that the
portfolio
so that the
portfolio  is self-financing. (Recall that the value
of the portfolio at time t is
is self-financing. (Recall that the value
of the portfolio at time t is 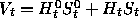 , and that the
portfolio is self-financing if
, and that the
portfolio is self-financing if  .)
.)
 ,
,
 ,
,
 .
.
27. Let 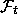 be the natural filtration
associated with Brownian motion (as in the proof of Theorem 8.4 of
lectures). Show that if X is an
be the natural filtration
associated with Brownian motion (as in the proof of Theorem 8.4 of
lectures). Show that if X is an  -measurable random
variable, then if
-measurable random
variable, then if  is a probability measure equivalent to that
of the Brownian motion, then the process
is a probability measure equivalent to that
of the Brownian motion, then the process

is a 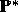 -martingale.
-martingale.
28. Use the Black-Scholes model to value a forward start option (described in Question 3).
29.
Suppose that the value of a European call option can be expressed
as 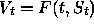 (as we prove in Proposition 9.2). Then
(as we prove in Proposition 9.2). Then
 , and we may define
, and we may define  by
by

Under the risk-neutral measure, the discounted asset price
follows 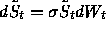 , where (under this
probability measure)
, where (under this
probability measure) 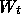 is a standard Brownian motion.
is a standard Brownian motion.
 .
.
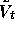 is a martingale under
the risk-neutral measure, find the partial differential equation
satisfied by
is a martingale under
the risk-neutral measure, find the partial differential equation
satisfied by  , and hence show that
, and hence show that
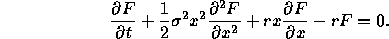
This is the Black-Scholes equation.
30. (Delta-hedging).
The following derivation of the Black-Scholes equation is very
popular in the finance literature.
We will suppose, as usual, that an asset price follows
a geometric Brownian motion. That is, there are parameters  ,
,
 , such that
, such that

Suppose that we are trying to value a European option based on this
asset.
Let us denote the value of the option at time t by  . We know
that at time T,
. We know
that at time T,  , for some function f.
, for some function f.
 , consists of
one option and a (negative) quantity
, consists of
one option and a (negative) quantity 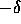 of the asset.
Assuming that
the portfolio is self-financing, find the stochastic differential equation
satisfied by
of the asset.
Assuming that
the portfolio is self-financing, find the stochastic differential equation
satisfied by  .
.
 for which the portfolio you have
constructed is `instantaneously riskless', that is for which the
stochastic term vanishes.
for which the portfolio you have
constructed is `instantaneously riskless', that is for which the
stochastic term vanishes.
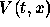 .
Notice that this is the Black-Scholes equation obtained in Question 29.
.
Notice that this is the Black-Scholes equation obtained in Question 29.
 , where v is a solution of the Black-Scholes
equation. Use Itô's formula to write down a stochastic differential
equation for U.
, where v is a solution of the Black-Scholes
equation. Use Itô's formula to write down a stochastic differential
equation for U.
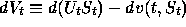 .
.
 . Use the stochastic differential
equation for
. Use the stochastic differential
equation for  and the Black-Scholes differential equation
(differentiated with respect to the x variable) to show that this is
equivalent to
and the Black-Scholes differential equation
(differentiated with respect to the x variable) to show that this is
equivalent to

Here 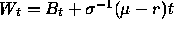 is a Brownian motion under the
risk neutral measure.
is a Brownian motion under the
risk neutral measure.